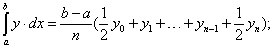Водоизмещение судна

ВОДОИЗМѢЩЕНІЕ СУДНА, выражается въ вѣсовыхъ или объемныхъ единицахъ; первое обозначается буквою D, второе — V; В. опредѣляетъ тотъ объемъ воды, к-рый вытѣсняетъ судно, погруженное по данную ватерлинію; т. к. судно въ зав-сти отъ состоянія нагрузки м. имѣть углубленіе выше и ниже грузов. в-линіи, то различаютъ нормальное В. и В. съ перегрузкой или недогрузкой. Зная, что 35 кб. фт. солен. и 36 кб. фт. прѣсной воды вѣсятъ около 1 тонны, путемъ простого дѣленія можно перейти отъ V къ D, подъ к-рымъ понимаютъ вѣсъ объема воды, вытѣсненной судномъ или, что то же по закону Архимеда, вѣсъ всего плавающаго корабля. Чтобы судно дан. размѣровъ плавало по требуемую грузовую в-линію, т.-е. имѣло дан. В., необходимо такъ распорядиться вѣсами составныхъ частей судна (корпуса, механизмовъ, вооруженія, бронированія и т. п.), чтобы общая сумма ихъ была точно равна В., вычисленному указан. ниже способомъ. Кривыя, опредѣляющія форму подвод. части к-бля, не м. б. выражены уравненіями; поэтому точное вычисленіе В. затруднительно. Обык-но пользуются приближенными способами интеграл. исчисленія для рѣшенія опредѣл. интеграловъ вида ∫∫y.dx.dz, к-рые въ свою очередь приводятся къ вычисленію простыхъ площадей вида ∫y.dx или ∫y.dz. Вычисленіе производится по слѣд. шаблону: получивъ нужное число площадей в-линіи или попереч. шпангоутныхъ сѣченій, принимаютъ эти площади за ординаты нов. площадей, просуммировавъ к-рыя, получаютъ искомое D. Практически эти выкладки сводятся къ составленію таблицъ, при чемъ для облегченія работы всѣ расчеты ведутся для половины корабля и результаты удваиваются. Для примѣра приводится наиб. простая табл. вычисленія В. по "способу трапецій". Какъ извѣстно, этимъ способомъ опредѣленный интегралъ вида

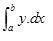
рѣшается такъ:

составивъ подходящую этому рѣшенію таблицу, заполняютъ ее данными теоретич. чертежа, т.-е. снимаютъ съ него ординаты (разстояніе отъ діаметр. пл-сти до обвода соотвѣтств. в-линіи на каждомъ шпангоутѣ) и помѣщаютъ въ подлежащія рубрики такой таблицы:

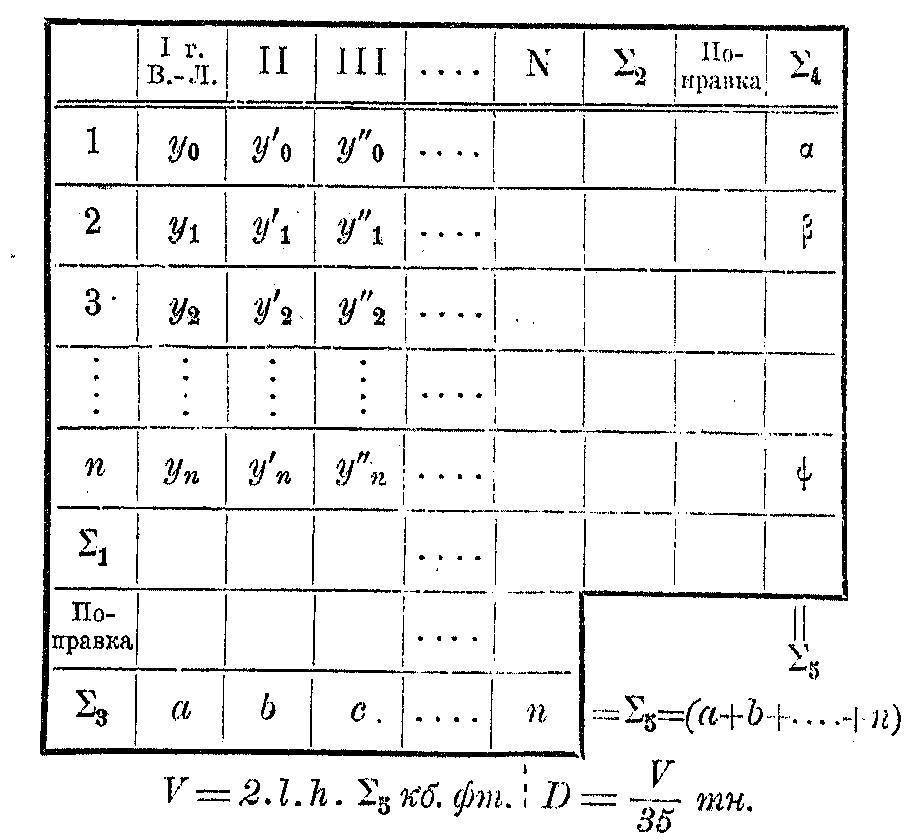
Здѣсь римскими цифрами I, II... N обозначены номера в-линій, арабскими 1, 2... n — номера шпангоутовъ, у, у′, у″ и т. д. — соотвѣтств. ординаты; ∑₁= суммѣ цифръ вертик. столбцовъ; ∑₂= суммѣ цифръ горизонтальныхъ столбцовъ; поправка = полусуммѣ крайн. ординатъ, напр., (y₀+y_n)/2; ∑₃ и ∑₄ — почленная разница цифръ строки ∑₁, строки ∑₂ и поправокъ, ∑₅ — окончательная сумма, l — разстояніе между в-линіями, h — разст. между шпангоутами. Точность вычисленія тѣмъ больше, чѣмъ чаще проведены горизонт. и вертик. сѣченія. Достаточная точность получается при 10 в-линіяхъ и 20 шпангоутахъ. Объемъ подвод. части судна имѣетъ свой ц. тяжести, к-рый на языкѣ корабельныхъ инж-ровъ называется центромъ величины. Въ этой точкѣ приложена вертик., вверхъ дѣйствующая сила гидростатич. давленія воды, равная D. Положеніе этой точки, опредѣляемой относ-но 3 коорд. пл-стей: пл-сти миделя, діаметр. пл-сти и пл-сти груз. в-линіи, играетъ важную роль въ вопросахъ остойчивости судна, а потому она всегда опредѣляется одновр-но съ вычисленіемъ В., пользуясь формулой моментовъ равнодѣйствующей и составляющихъ. Разстояніе "центра величины" отъ груз. в-линіи

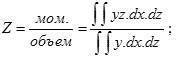
разстояніе ц. в. отъ миделеваго сѣченія

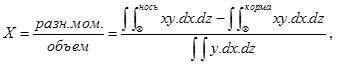
а разстояніе до діаметр. пл-сти у=0, по симметричности судна. Значокъ 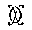обозначаетъ мидель, т.-е. среднее попереч. сѣченіе к-бля. Вышеприведенная таблица пополнится новыми рубриками "плечъ" и"моментовъ" относ-но сказанныхъ пл-стей. Для опредѣленія Z будемъ имѣть: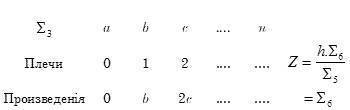

Для опредѣленія X берется разность носовыхъ и кормовыхъ моментовъ:

Въ этихъ таблицахъ ∑₃ и ∑₄ взяты цѣликомъ изъ ранѣе приведенной таблицы вычисленія В. Часто употребляется для этихъ вычисленій формула Симпсона, к-рая даетъ болѣе точные результаты, но зато и требуетъ болѣе сложныхъ выкладокъ. Въ наст. время, съ усоверш-ніемъ ариѳмометровъ и планиметровъ, работа сводится до минимума, а при работѣ съ планиметромъ отпадаетъ ординатное вычисленіе площадей, и въ таблицы вносятся въ соотвѣтств. рубрики прямо отсчеты планиметра, т.-е. площади или пропорціон. имъ величины.